
d20 Dice Randomness Test: Chessex vs GameScience
Do Your Dice Roll True?
 The founder of GameScience, Lou Zocchi, has long claimed that GameScience dice roll more true than other gaming dice. In a well-known GenCon video Zocchi explained why GameScience dice should roll more true.
The founder of GameScience, Lou Zocchi, has long claimed that GameScience dice roll more true than other gaming dice. In a well-known GenCon video Zocchi explained why GameScience dice should roll more true.
His logic is that due to how dice are made, traditional RPG dice are actually put through a process similar to a rock tumbler as part of the painting and polishing, and this process causes the dice to have rounded edges. In theory the uneven rounding gives the dice an inconsistent shape that favors certain sides. GameScience dice are not put through this process, which is why they retain their sharp edges and is also why their dice come uninked.
While Zocchi’s makes a good argument about egg-shaped d20s, what was lacking was any kind of actual testing of how the dice roll. Nowhere were we able to find any tests of d20s — either GameScience or traditional d20s — to determine whether or not they roll true. As giant fans of dice and an impartial third party, we decided to run a test ourselves and see just how randomly RPG d20s really roll.
We pitted GameScience precision dice against Chessex dice (the largest RPG dice manufacturer) to see what science has to say.
Methodology
For the principle test we used one Chessex d20 and one GameScience d20, both brand new right out of the packaging. The GameScience d20 was inked with a Sharpe to make it easier to read the results, but the dice were not modified in any other way.
The dice were rolled by hand on a battlemat on a level table. For this experiment the dice were rolled on the surface for at least two feet and had to bounce off a flat backstop before coming to rest. This is similar to the requirements of craps tables in casinos. Our logic is that if this method successfully prevents cheating with six-sided dice, it will more than suffice for d20 dice being rolled without any intent to alter the results. (Since casinos are not losing money on gambling, we assume they know what they’re doing).
Each die was rolled 10,000 times, and the results recorded.
Test Results
After an insane amount of dice rolling, here is a quick look at the results for each die:
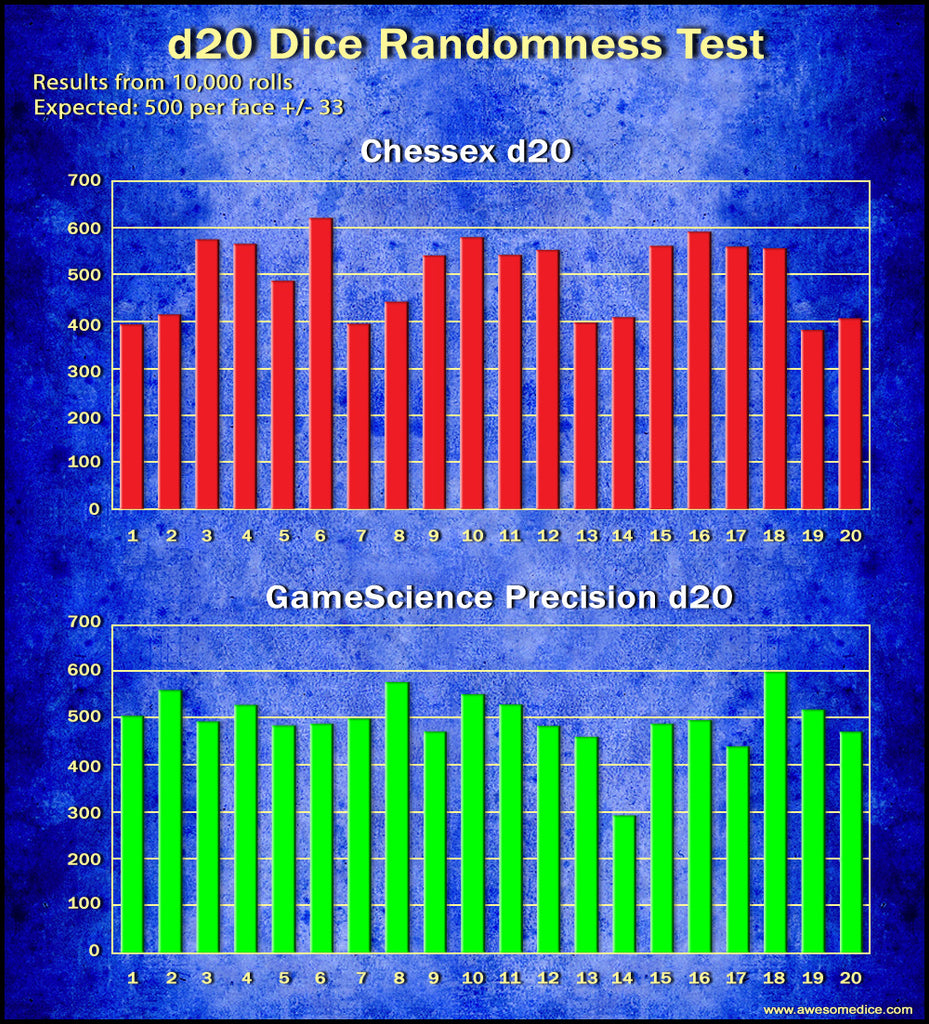
A casual analysis of the results suggests that neither die is rolling randomly.
If we had a d20 that rolled perfectly, each face would come up 500 times. But of course randomness isn’t perfect and we’d expect some deviation: over the course of 10,000 rolls we’d expect, with 85% confidence, that each face would be within about 33 of 500 — so anywhere from 467 to 533 is within the bounds of randomness. (At 95% confidence the margin of error is 45). Neither die falls within these bounds.
The Chessex d20 had a standard deviation of 78.04, and the GameScience d20 had a standard deviation of 60.89.
While neither die rolled true, it’s certain that the Chessex die rolled less true, with a greater degree of deviation from the expected range across more of the dice faces. Interestingly, the GameScience die actually rolled very close to true except for the number 14 which rolled vastly less often than it should have, farther off than any face of the Chessex d20. Applying the results to a Chi Squared test also confirms that neither die is rolling randomly (even if you ignore the 14/7 on the GameScience die).

GameScience 14 Theory:
We have a theory as to why the 14 rolled so infrequently on the GameScience d20. Every GameScience die has a small chunk of plastic that sticks out of one face. This flashing is from where the die was removed from the mold. It occurs on all dice, but in Chessex dice this flashing is removed in the polishing process.
On GameScience 20-sided dice this flashing is on the 7 face — directly opposite the 14.
It seems likely that it is more difficult for the d20 to land on the face with the flashing sticking out, pushing the GameScience die off that face. In other words, this flashing makes the 14 roll far less often than it should. Since the flashing position is set from the mold, all GameScience d20s should have the flash in the same position (and all in our inventory do).
Some Confirmation
Since this test was simply one d20 from both manufacturers, it’s possible we just happened to choose the only Chessex d20 that didn’t roll true, and the only GameScience d20 that rolled far fewer 14s. As a check on our results we took another new d20 from both Chessex and GameScience and rolled each under the same conditions.
After 1,600 rolls the same pattern emerged (incidentally, the standard deviation after 1,600 rolls was almost identical to the 10,000 roll test). The Chessex d20 still had more deviation from expected than GameScience, and the GameScience d20 rolled massively fewer 14 results. Both dice still rolled sufficiently out of true to be beyond the margin of error. So this quick (well, not so quick) double check is some confirmation of the 10,000 roll test.
So Which Dice Are Better?
It’s worth stressing that based on our tests you would need a lot of dice rolls before you saw a meaningful difference in any of these gaming dice — roll a thousand times and maybe you’ll see 5 or 10 less of a given number than you’d expect (or more). So for gaming purposes both dice will work just fine. Seriously.
But that said Chessex dice (and in theory any rounded-edged dice) are going to roll less close to true. Because of the randomness of the process that changes the shape of the dice, there’s no way to predict which faces are going to roll better or worse. Indeed this means that you could have dice that are “lucky” and roll high more often or crit more often, and “cursed” dice that seldom roll 20s and fumble more often.
With GameScience dice, on the other hand, you know that the 14 will roll substantially less than any other result — so technically the dice will roll low, but the 20 should roll just about as often as the one, or the 10. If you carefully cut off the bump on the GameScience dice with a sharp box cutter or Exacto knife you should get a result that is very close to being truly random.
Raw Data
Here is all of the data from the 10,000 roll test, so anyone who wants can subject the numbers to their own statistical analysis. We’re including in here the percentage that the rolls of any given number deviate from the expected number of 500 per face.
Chessex d20 |
||
| Number | Qty Rolled | Deviation from Expected |
| 1 | 395 | 21.00% |
| 2 | 417 | 16.60% |
| 3 | 576 | 13.19% |
| 4 | 567 | 11.82% |
| 5 | 488 | 2.40% |
| 6 | 622 | 19.61% |
| 7 | 396 | 20.80% |
| 8 | 443 | 11.40% |
| 9 | 542 | 7.75% |
| 10 | 581 | 13.94% |
| 11 | 544 | 8.09% |
| 12 | 554 | 9.75% |
| 13 | 399 | 20.20% |
| 14 | 411 | 17.80% |
| 15 | 562 | 11.03% |
| 16 | 593 | 15.68% |
| 17 | 561 | 10.87% |
| 18 | 558 | 10.39% |
| 19 | 383 | 23.40% |
| 20 | 408 | 18.40% |
GameScience d20 |
||
| Number | Qty Rolled | Deviation from Expected |
| 1 | 508 | 1.57% |
| 2 | 564 | 11.35% |
| 3 | 496 | 0.80% |
| 4 | 532 | 6.02% |
| 5 | 488 | 2.40% |
| 6 | 492 | 1.60% |
| 7 | 503 | 0.60% |
| 8 | 580 | 13.79% |
| 9 | 474 | 5.20% |
| 10 | 555 | 9.91% |
| 11 | 533 | 6.19 |
| 12 | 486 | 2.80% |
| 13 | 463 | 7.40% |
| 14 | 295 | 41.00% |
| 15 | 491 | 1.80% |
| 16 | 499 | 0.20% |
| 17 | 443 | 11.40% |
| 18 | 602 | 16.94% |
| 19 | 522 | 4.21% |
| 20 | 474 | 5.20% |
This is Just One Test
In the world of science, this is just one very small test. To have relatively certain results we’d need to replicate this test across many different Chessex and GameScience dice — if anyone is interested in running their own test to corroborate or contradict our results, we would love to hear about it!
Once our wrists recover from all the rolling, we may consider a second test ourselves — specifically to confirm the theory that the flash on the GameScience die is what is causing the 14 to roll so low: we want to carefully sand the flash down and retest the same die to see if it then rolls more true.
Disclaimer: we have made every effort to ensure that our testing methodology was as fair and accurate as possible; however, without much more testing we cannot say with certainty whether one kind of dice roll better or worse.




I had seen another roll test of 10,000 and the pattern of occurrence lines up with the physicality of the die for Chessex. Your test shows the same pattern. The article came to the wrong conclusion that the chessex die was truly random. If you hold the die between thumb and forefinger, with the thumb on 1 and the finger on 20, you were touching the two points of low probability. The three numbers touching the triangular sides of the 1(7,13,19) and the 20 (2,8,14) were the next tier of probably, leaving 12 remaining faces that had relatively even levels of probability. Look at the red bar graph (1 & 2,7 & 8,13 & 14,19 & 20) are all at an obvious lower occurrence. The die must bulge slightly. Also, the rounded, cornerless-pointless edges of the Chessex allow it to roll and roll and roll allowing the tiny weight imbalance of the die to have greater influence. Chessex dice will roll and even change or reverse direction while rolling. When I see a live stream where the die keeps rolling and the people are waiting for it to stop—I know that’s probably a Chessex die or another rounded edge manufacturer. There is a clear pattern to rolling and Chessex roll fewer 1’s and fewer 20’s.
Royal F. on
Wow, that was a lot of work. Congrats on that! But that mold point blemish on the GameScience die should be smoothed with a model-grade sandpaper. After that, it will roll much more precisely. Let us know if you decide to do that and update the tests!
Clauber Alex on
A friend of mine actually did his science fair project on Game Science dice a few years ago. He got 10 Game Science d20s, rolled them each 5,000 times. Put them in a tumbler for a while and rolled again. He repeated that 4 or 5 times until the dice were pretty well rounded.
He saw the 7/14 issue on all of the dice, and it got better (more true) with the tumbling. He didn’t test any non-Game Science dice, but I’d wager the rounded dice are actually better overall.
Steve Hammond on
Based on the results of the 10k test, if you add all percentage deviations of each die and divide each number by 20 (for each face/number), these are the results:
Chessex: Average is 14.2%
GameScience: Average is 7.519%
Would this mean that the Gamescience die rolled closer to true than the Chessex die did? Furthermore, if the flash on the GameScience die was adjusted accordingly, the accuracy would increase even more.
Thank you for this article!
Bryan Borne on
I bought several sets of Gamescience dice [clear, yellow, amber, orange, red, blue] back in around 1980 or so, as a result of the “2# Stacks of D20” size-coherence adverts in Dragon™ magazine. The D20, at that time, was numbered 0-9 twice. I still use them as my preferred dice, and they are still going strong, with almost no damage whatsoever from wear & tear.
Christopher Andrew Simpson on